The Theory \ Details \ appendices \ appendix B

Appendices

Appendix B. Downside Volatility

Let’s start by selecting a value for the continuously compounded minimum acceptance excess rate (MAR). Downside volatility takes into account only those values of observed excess rates of return that lie below MAR. In other words, downside volatility is a measure of risk, defined as volatility below MAR.

Definition. Downside volatility , corresponding to selected value

of MAR, is defined as

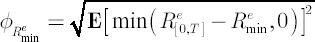where

denotes chosen investment horizon.

Note. In the case of the corresponding downside volatility measure is called semi-volatility.

Note. Compare semi-volatility definition to an expression for volatility :

Obviously, if is symmetrically distributed, then volatility is equal to semi-volatility multiplied by 2.

If a distribution of logarithmic returns deviates from normality, then downside volatility is a more preferable risk measure than often more common volatility measure. Most evident advantage of downside volatility is its
ability to give a proper weight for possible asymmetry in distribution of returns measured with skewness. But with the proper choice of MAR the downside volatility can also reflect possibly positive kurtosis excess in price increments.

From the practical point of view, downside volatility is better suited for portfolio risks measurement , since virtually all investors are tolerant to sudden upside movements in wealth, while tending to avoid corresponding downside movements.

Normalized Downside Volatility

In practice, it is more convenient to use an adjusted measure of downside volatility, called normalized downside volatility. Under the assumptions of the analytical model normalized downside volatility coincides with

.

Definition. Normalized downside volatility

, corresponding to value

of MAR, is defined as

where

, and

and

stand for standard normal density and distribution function respectively.