The Theory \ Details \ appendices \ appendix C

Appendices

Appendix C. Investments ranking and Performance measures

Most of the existing measures, destined to evaluate performance of a portfolio or an individual asset, have the form of Risk-to-Reward ratio. They differentiate depending on particular definitions of Risk and Reward.
Choices of risk and reward, utilized in SmartFolio, are summarized in the following table.

	Reward
Risk	Expected excess growth rate	Excess Mu
Volatility	Information Ratio	Instantaneous Information Ratio
Downside Volatility	Sortino Ratio	Instantaneous Sortino Ratio
Normalized Downside Volatility	Normalized Sortino Ratio	Normalized Instantaneous Sortino Ratio
Conditional Value-at-Risk	STARR Ratio	Instantaneous STARR Ratio
Normalized Conditional Valueat- Risk	Normalized STARR Ratio	Normalized Instantaneous STARR Ratio

Fix some minimum acceptance excess rate

. In the following context the latter is also is also called Target Excess Rate.

Information Ratio

Definition. Information Ratio

, corresponding to

, is equal to the difference between expected excess growth rate and

, divided by volatility:

Note. Widely recognized Sharpe Ratio is a particular case of information ratio corresponding to

Sortino Ratio

Definition. Sortino Ratio

, corresponding to

, is equal to the difference between expected excess growth rate and

, divided by downside volatility with MAR equal to

Normalized Sortino Ratio

Definition. Normalized Sortino Ratio, corresponding to

, is similar to Sortino ratio, but with normalized downside volatility in denominator:

Under the assumptions of the analytical model, the normalized Sortino ratio coincides with information ratio.

STARR Ratio

Definition. STARR Ratio is equal to the difference between expected excess growth rate

and

, divided by the Conditional Value-at-Risk, transformed to logarithmic return:

Normalized STARR Ratio

Definition. Normalized STARR Ratio (NSTARR) is the STARR ratio, corrected in such a way that in case of normally distributed logarithmic returns it coincides with information ratio.

where

denotes Normalized CVaR.

Definition. Normalized CVaR is a measure, based on CVaR, corrected in such a way that under the assumptions of the analytical model it coincides with volatility measure.

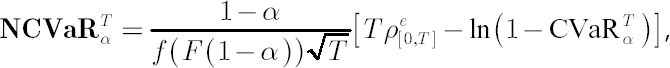
where

and

are standard normal density and distribution function respectively.

Under the assumptions of the analytical model, all above performance measures are equivalent when used to sort the list of available portfolios according to their investment attractiveness. Otherwise, because of the
properties of downside volatility and CVaR respectively, the Sortino Ratio and the STARR ratio might become more relevant measures of performance.

Standard performance measures vs. their instantaneous counterparts

Below we focus on the Sharpe ratio, but the same logic holds true for all other performance measures, presented above.
Definition. Sharpe Ratio

is equal to the expected excess growth rate divided by volatility:

Definition. Instantaneous Sharpe Ratio

is equal to excess Mu divided by volatility:

Both the Sharpe ratio and the instantaneous Sharpe ratio sort assets according to their relative performance in the past. However, there is an essential distinction in the information the corresponding rankings reflect.

If compared assets are supposed to be used as components of a continuously rebalanced portfolio, then the instantaneous Sharpe ratio becomes more appropriate performance measure.
If one compares already formed portfolios, rather than separate assets, then their relative investment appeal should be measured with the Sharpe ratio.

In the former case, when selecting portfolio components, the investor has an opportunity of combining them with each other and with the riskless asset. On the contrary, in the latter case one considers the portfolios
as separate alternative investments, thus depriving the investor of the continuous rebalancing advantages. For further details see [Nielsen, Vassalou; 2004].