Portfolio Optimization
Efficient frontier
Definition. The portfolio  , which maximizes the expected value of CRRA utility function for some value of relative risk aversion coefficient, will be called CRRA-optimal or CRRA-efficient. , which maximizes the expected value of CRRA utility function for some value of relative risk aversion coefficient, will be called CRRA-optimal or CRRA-efficient.
Definition. The efficient frontier is the entire set of all CRRA-optimum portfolios.
Note. The definition, mentioned above, differs a little bit from the classical definition of the efficient frontier as the entire set of portfolios, which are optimal according to Mean-Variance criterion. If assumptions of the
analytical model hold true, then by virtue of the result, formulated in the previous section, these two definitions coincide. In the general case, however, the above sets can differ. Our definition of the efficient frontier may be more suitable here since the maximization of expected utility better corresponds to the purposes of an investor, than does maximization by the means of Mean-Variance criterion.
Graphic representation of the efficient frontier is the corresponding curve on the Risk-Reward plane. Within the framework of the analytical model and convex constraints on the set of admissible portfolios this curve is
convex; in general case, however, the above convexity property might be violated.
Depending on the purposes of the analysis, definitions of Risk and Reward measures, which correspond to the axes on the chart, can vary. Below we present variations of such measures that are realized in SmartFolio package.
Portfolio Risk measures
Portfolio Reward measures
- Excess Mu

- Expected excess growth rate

Note. In a single-period framework it is common to restrict the admissible portfolios to fully-invested portfolios only. In a multi-period framework it often makes sense to omit this restriction, in particular if the
portfolio expected excess growth rate is chosen as a Portfolio Reward measure.
Definition. If the set of admissible portfolios is restricted to fully-invested portfolios only, then the corresponding efficient frontier will be denoted as FI-efficient frontier.
Examples of FI-efficient frontier graphs for each of the two previously defined measures of portfolio reward and  chosen as the portfolio risk, are shown below. Additional elements on the first graph refer to the subsequent topics. chosen as the portfolio risk, are shown below. Additional elements on the first graph refer to the subsequent topics.

The rest of the chapter is devoted to the analytical model case, where the notions of CRRA-efficiency and Mean-Variance efficiency coincide.
Analytical model: Efficient Frontier generation
Consider Risk-Adjusted Expected Excess Rate of Return  corresponding to the relative risk aversion coefficient corresponding to the relative risk aversion coefficient 
The efficient frontier can be parameterized by  in the following way: in the following way:
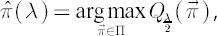
where  denotes the admissible portfolios set. denotes the admissible portfolios set.
Note. If portfolio  lies on FI-efficient frontier, and no other constraints are imposed on lies on FI-efficient frontier, and no other constraints are imposed on  , then implied value of , then implied value of  that makes that makes  optimal for optimal for  is is  . .
Analytical model: Global Minimum Variance portfolio
Definition. The Global Minimum Variance (GMV) portfolio is a fully-invested portfolio with the minimum volatility value  . .
The GMV portfolio belongs to FI-efficient frontier and is located on its left end. If no constraints are imposed on  apart from the full-investment condition, then the GMV portfolio allows for the analytical representation: apart from the full-investment condition, then the GMV portfolio allows for the analytical representation:

where  is is 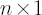 vector of ones. vector of ones.
The corresponding values of  and and  are calculated according to the following expressions: are calculated according to the following expressions:

Analytical model: Tangency portfolio
Definition. The targency portfolio is a fully-invested with maximum value of Instantaneous Sharpe Ratio.
Definition. The straight line on the graph 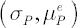 , passing through the origin and being a tangent to FI-efficient frontier, is called the Capital Market Line (CML). , passing through the origin and being a tangent to FI-efficient frontier, is called the Capital Market Line (CML).
The tangency portfolio corresponds to the point, where CML touches the FI-efficient frontier.
If no constraints are imposed on  apart from the full-investment condition, then: apart from the full-investment condition, then:
- Tangency portfolio
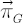 admits the analytical representation: admits the analytical representation:
where  is is 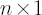 vector of ones. vector of ones.
- Formulas for
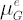 and and  have the following form: have the following form:
- Any portfolio on the FI-efficient frontier can be obtained as a linear combination of the GMV portfolio and the tangency portfolio.
- If the full-investment condition is omitted, then the renewed efficient frontier coincides with Capital Market Line. Any portfolio, belonging to CML, can be represented as a linear combination of a riskless asset and a tangency portfolio. The latter statement has a title of the Two-Fund Separation Theorem.
Two-Fund Separation Theorem
Theorem. Assume the following conditions hold:
- There are no constraints imposed on admissible portfolios
- Riskless asset is the same for all investors
- Risk-free rates for lending and borrowing are equal
- There are no transaction costs and taxes
Then any portfolio belonging to the efficient frontier is a combination of the tangency portfolio and a riskless asset.
Two-Fund Separation Theorem serves as a theoretical basis for index funds activity. Indeed, if Two-Fund Separation Theorem holds, then all rational investors regardless of their risk profile hold the same mix of risky securities. Therefore, the market share of each asset is equal to its weight in the tangency portfolio. In other words, any rational investor who isn’t faced with portfolio constraints would hold all of his funds in a riskless asset and in a mutual fund that replicates the market portfolio.
| |
|

 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
portfolio optimization
\
efficient frontier
The Theory
\
Details
\
portfolio optimization
\
efficient frontier








 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
portfolio optimization
\
efficient frontier
The Theory
\
Details
\
portfolio optimization
\
efficient frontier