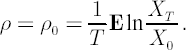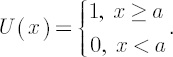Portfolio Optimization
Utility functions
The utility function describes the dependence between the amount of wealth obtained by the investor, when reaching the investment horizon, and that "usefulness" the investor can extract from it. Usefulness itself is
measured in some abstract units. The shape of the utility function gives a notion of what exactly the investor puts in the "risk" concept. The optimal investment problem consists in finding the portfolio strategy that maximizes the expected value of the utility function at some predetermined moment in the future.
Utility Functions Properties
- The utility function is an increasing function of wealth.
Obviously, with growth of wealth usefulness that investor can extract from it, should grow also,
therefore it is advisable to limit oneself to consideration of increasing utility functions only.
- The utility function is concave.
It is easy to see that the investor, who is averse to risk, will have a concave function of utility.
Indeed, let’s consider the following game: the wealth of the investor at time  is equal to is equal to  . At time . At time 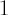
two outcomes are possible:
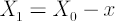 with the probability with the probability 
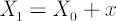 with the probability with the probability 
This game is fair in the sense that the expected game profit is equal to zero: 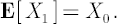 However for an investor with a concave utility function However for an investor with a concave utility function 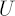 such game will appear unfavorable. Indeed, such game will appear unfavorable. Indeed,
by the definition of concavity
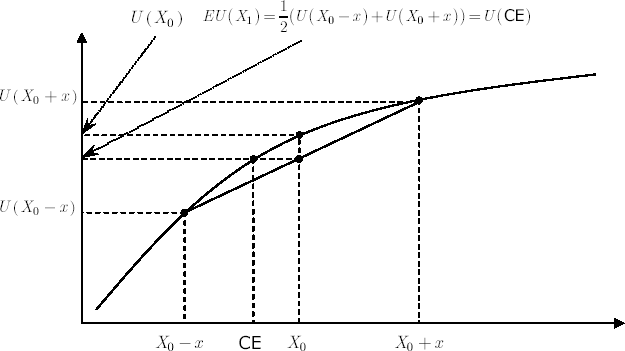
Graphical representation of the game is represented in figure 1.
The quantity called Certainty Equivalent, which is defined by the expression 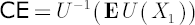 , is also shown there. , is also shown there.
Definition. Certainty Equivalent (CE) is a minimum amount of wealth, guaranteed preservation of which allows the investor to decline the proposed game.
Figure 1. Graphical representation of a fair game for an investor with a concave utility function.
The degree of concavity for a given utility function is determined by the so-called Risk Aversion Measures.
Commonly used Utility Functions
- Quadratic Utility
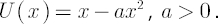
Used to obtain Mean-Variance optimal portfolios in Harry Markovitz single-period framework.
- Power Utility
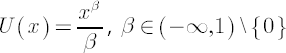
The maximization of expected value of such utility function at time 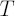 is equivalent to the maximization of the expected rate of return is equivalent to the maximization of the expected rate of return 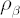 , compounded , compounded 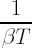 times per annum: times per annum:
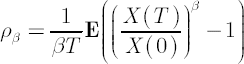 , where , where 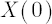 and and 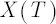 denote the initial and terminal wealth respectively. Values denote the initial and terminal wealth respectively. Values 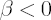 correspond to the notion of discount rate. With decrease in correspond to the notion of discount rate. With decrease in 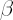 the the
investor’s risk tolerance also decreases.
- Logarithmic Utility
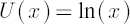
It can be considered as a limiting case of a power utility function as 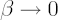 . It is used for the maximization of expected continuously compounded growth rate: . It is used for the maximization of expected continuously compounded growth rate: 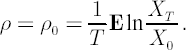
- Exponential Utility
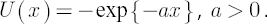
- Level reaching indicator
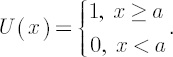
It is used for the maximization of the probability of reaching the given amount of capital (in the so-called problems of hedging with probability, smaller than one).
| |
|

 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
portfolio optimization
\
utility functions
The Theory
\
Details
\
portfolio optimization
\
utility functions








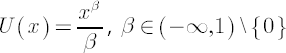
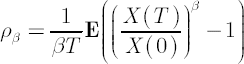 , where
, where