Risk Management Tools
Definitions
Value-at-Risk (VaR) and Conditional Value-at-Risk (CVaR, other notations include Expected Shortfall, Expected Tail Loss, Tail VaR) are indispensable tools of portfolio risk management.
VaR and CVaR measures become increasingly useful when the distribution of portfolio logarithmic returns substantially deviates from normal. In this case, volatility as a common risk measure appears inappropriate.
Portfolio VaR is defined as a maximum portfolio loss (measured in % of initial wealth) over a given time interval at a given level of statistical confidence.
Definition. 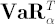 is implicitly defined by the following expression (for simplicity we assume that portfolio returns have continuous distribution): is implicitly defined by the following expression (for simplicity we assume that portfolio returns have continuous distribution):
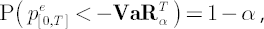
where 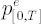 is portfolio excess simple return over is portfolio excess simple return over 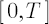 period. period.
To put it more formally, 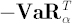 corresponds to the corresponds to the 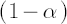 -quantile of the distribution of portfolio excess simple return over -quantile of the distribution of portfolio excess simple return over 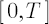 period. period.
Portfolio CVaR is conditional expectation of losses beyond VaR.
Definition. 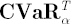 is an expected value (with opposite sign) of portfolio excess simple return is an expected value (with opposite sign) of portfolio excess simple return 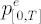 under the condition under the condition 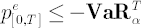 : :
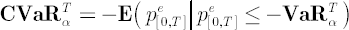
In other words,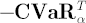 is an average value of is an average value of 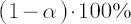 of highest losses. Common values for of highest losses. Common values for 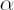 are 0.9, 0.95, 0.975 and 0.99. The time horizon are 0.9, 0.95, 0.975 and 0.99. The time horizon 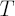 corresponds to a period required for complete liquidation of all portfolio positions. corresponds to a period required for complete liquidation of all portfolio positions.
Figure 1. Distribution of logarithmic portfolio returns over the period 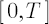 . .
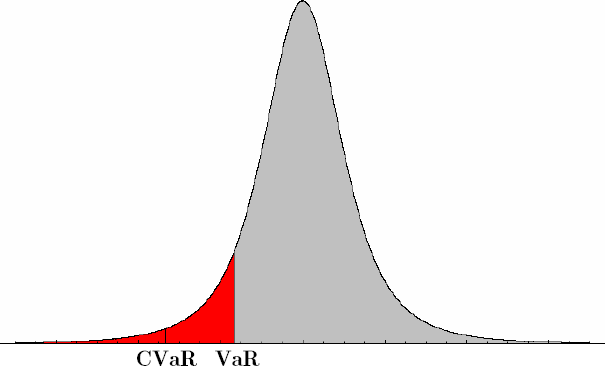
Important! Although CVaR isn’t so widespread a measure of risk as VaR, in contrast to VaR it possesses important property of subadditivity. Subadditivity of CVaR means that CVaR of simultaneously holding two
portfolios is less or equal to the sum of CVaRs for individual portfolios, considered separately. That’s why CVaR is more suitable quantity to be included in portfolio optimization (as constraint or part of an
optimization criterion) than VaR is. Essential shortfalls of VaR as a measure of risk due to a lack of subadditivity are discussed in detail in [Artzner, Delbaen, Eber, Heath; 1999].
| |
|

 SiteMap\
SiteMap\ Contact Us
Contact Us
 The Theory
\
Details
\
risk management tools
\
definitions
The Theory
\
Details
\
risk management tools
\
definitions